User interaction in a three-dimensional OpenGL scene often includes “picking”, which means that a user can select an object in the scene by clicking on it. This requires to find out the correct object in the three-dimensional scene from the two-dimensional information that is provided for this user interaction event – the x and y coordinate of the click.

There are several strategies to do so:

• using the GL_SELECTION render mode
• rendering each primitive with a unique color and using glReadPixels
• using a “picking ray”

For a recent project I chose to implement ray-based picking because it does not require to fiddle around with the OpenGL API and it is fast and easy to implement if you only need to identify if an object was selected by a certain radius around its center point. The idea is that you cast a ray from the point the click occured on the screen (i.e. on the “near plane” of the OpenGL view frustum) into the 3D scene and then you check the distance between the ray and an object’s center point. The basic recipe is as follows:

1. Calculate normalized coordinates from screen coordinates

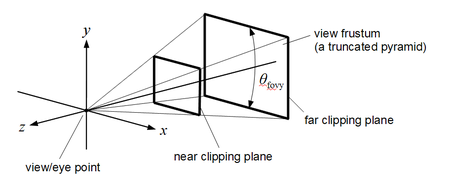OpenGL view frustum, Martin Kraus, Wikimedia Commons

Usually the window system will return the click location in screen coordinates with pixel values, where the top left corner is at (0, 0) and the bottom right corner is at (W, H), with W and H being the respective screen resolution values. These values need to be transformed to normalized coordinates with values between (-1,-1) at the bottom left corner (note that the y-axis needs to be inverted for that) and (1, 1) at the top right corner of your OpenGL viewport.

This can be done as follows with l as click location in screen coordinates, l’ as normalized click location and view.x and view.y, view.w and view.h describing the OpenGL viewport offset and size:

l'.x = (2 * (l.x - view.x) / view.w) - 1
l'.y = -((2 * (l.y - view.y) / view.h) - 1)     // invert axis

2. Calculate the “unproject” matrix

In order to calculate the “picking ray” later, we will need to create an “unproject” matrix. We know that the rendering of an OpenGL scene requires a model-view transform matrix M that describes the position of an object in the 3D scene and a projection matrix P that is needed to project the 3D scene onto a 2D view plane, which is what the user finally sees. In order to cast a ray from the 2D click coordinates into the 3D scene, we need to invert this transformation. As the final result, we can imagine being “inside” the 3D scene at the spot of the object (the coordinate system’s origin) and a ray is cast from a 2D plane (the view plane) towards us (the object). It’s a bit like the Truman show – you just changed seats from the viewer’s perspective to Truman.

In order to achieve this “change of perspective”, we just need to create the inverse of the model-view-projection matrix to create the “unproject” matrix U:

U = inverse(P * M)

3. Cast a ray into the 3D scene

Now we have all information to create the picking ray. We will calculate the beginning and the end point of the picking ray that runs from the near plane of the OpenGL view frustum to the far plane. In order to do so, we create these two points as 4-component vectors using our normalized screen coordinates l’. One vector is set with z = 0 (near plane) and one is set with z = 1 (far plane):

L_near = vector4(l'.x, l'.y, 0, 1)
L_far = vector4(l'.x, l'.y, 1, 1)

By multiplying our “unproject” matrix U with these points, we create the beginning and end points of our ray:

R_near = U *  L_near
R_far = U * L_far

We convert the 4-component vectors to 3-component vectors to use them later in the distance calculation:

R3_near = vector3(R_near.x / R_near.w,
                  R_near.y / R_near.w,
                  R_near.z / R_near.w)
R3_far = vector3(R_far.x / R_far.w,
                 R_far.y / R_far.w,
                 R_far.z / R_far.w)

4. Calculate the distance between the ray and the object

Now that we have our picking ray, we have to solve the problem of a point-line distance in 3D space between our ray and the object. Remember that our object is now located at the origin (0, 0, 0), because the model-view transform was involved in our “unproject” matrix. This simplifies the point-line distance formula to:

d = length(cross(R3_near, R3_far)) / length((R3_far - R3_near))

Now we finally have the distance d from the picking ray to the object (which is at origin (0, 0, 0)) in OpenGL units! You can now check if the user clicked the object around a specific radius d_max. Because calculating the length of a vector usually involves a square root operation, you can further speed up things by calculating the squared distance (i.e. omitting the square root operation).